| Package | Version | Citation |
|---|---|---|
| keras | 2.16.0 | @keras |
| safetensors | 0.2.0 | @safetensors |
| tensorflow | 2.20.0 | @tensorflow |
Convolution
Consider that you live in a high rise apartment complex. Did you hear that ambulance go by? How did the sound of the siren change as the ambulance approached towards your dwelling and then went past it to get lost amidst the surrounding buildings again?
The siren’s emitted sound is always the same. It is the local surroundings and the geometry of the echoes that brings the same sound to your ears again and again, but in altered/weighted form. The sound from the ambulance goes all around, hits on or other of the buildings, reflects, and comes back to your ears after a delay and weighted by the strength of the echo geometry.
What you hear is the overlapping of multiple, weighted copies of the sound emitted by the ambulance. As long as you have direct, i.e. non-reflected path from the ambulance to your ears, the echoes are relatively subdued. Once the vehicle gets right into your building complex and you lose the direct line-of-sight path, the echoes take over and the sound becomes a very confused mass that is barely recognizable.
What is Convolution?
All right, what does this have to do with convolution? Let us make some definitions first:
The free-space medium plus the buildings and other things that reflect sound in our environment, are called the “Channel”. The channel acts as a conduit between a source (transmitter) and a receiver.
The geometry of the echoes that connect transmitter to receiver, including the bounces of the walls, the resulting path-delays, and weighting are together denoted as the impulse response of the channel. This is what the channel would put out at the receiver if the source transmitter were to emit a very-short-duration signal, like the squeak of a mouse.
Now, most signals emitted by a source are usually not “squeak-like”: the ambulance has a siren that continuously emits the wellknown sound. Such a continuous signal is capable of mathematically decomposed into a series of “squeak-like” signals, which we call impulses.
So finally:
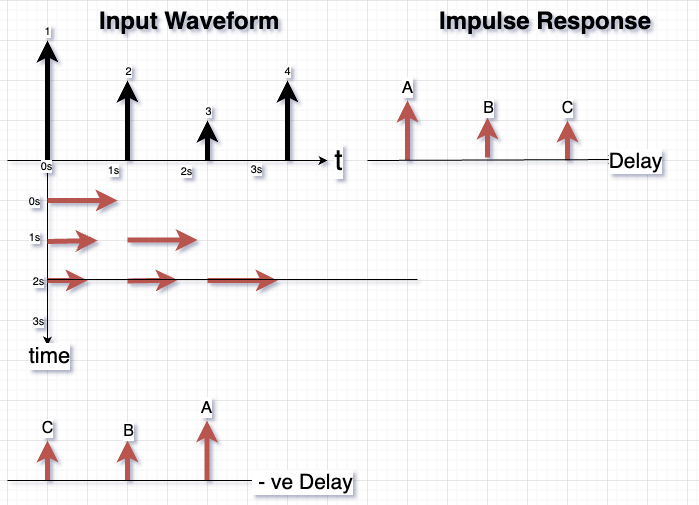
Each impulse undergoes the same geometry path-delays and path-weightings posed by the channel impulse response. This is diagrammatically shown below:
We see that impulses in the input waveform that arrive later undergo weighting by the earliest of path-delays and path-weightings. This should give you the intuition, that mathematically, this is like taking a weighted average but with the sequence of weights inverted in time!!! (This will become more obvious when we speak of the Wedding Lunch Metaphor below!)
If \(in(t)\) is the emitted sound waveform, and \(f(t)\) is the channel impulse response, we write the output of the channel as:
\[ \Large{out(t) = \int_{-\infty}^{\infty} in(t) * f(t-\tau) *d\tau} \tag{1}\]
Note that we are integrating wrt delay \(\tau\); and \(f\) uses negative \(\tau\) as its variable. Hence it is hence inverted in time, as shown in the bottom left of the Figure 1.
A Wedding Lunch Metaphor
Let us develop a better intuition for Convolution.
Consider a …nice fat South Indian Wedding. Lots of food, music, relatives, gossip, and of course the bride and groom. The main events are of course the Kashi Yatra, the Oonjal, the Tying of the Thaali, followed by Saptapadhi and so on. Let us say there are some 100 guests who are present and that it being a weekday, they wish to bless the couple and get back to work. So they wait for the the Tying of the Thaali, toss the rice into the air in the general direction of the couple, and…off they go to the huge Dining Hall, where the Marriage Feast of a meal awaits them. Since they are the first to enter the Dining Hall, they are referred to as the first pankti for the meal. With a large number of invitees, there would be 3-4 panktis before everyone has eaten.
Very well, 100 Guests enter the Dining Hall, and are briskly served by the smart serving staff. A South Indian Wedding Feast has many Courses and saatvik dishes, starting with paayasam, rice, pulses, ghee, sambhaar, more rice, rasam, veggies, paapad, curd, pickles, and finally dessert, with very many small side dishes in between. Each course is served in sequence, one after the other. The first pankti gets the first serving of each course, then the second pankti, and so on.
Let us say that the Dining Hall has a capacity for 150 people, and that there are 50 seats still vacant. When all the wedding ceremonies are done, some 50 Late Guests now would approach the pandal, bestow gifts on the couple, and THEN head for the Dining Hall. Now these 50 will be seated in the 50 vacant seats, and serving begins for them.
So after a while the Head Cook appears majestically at the doorway of the Kitchen, to survey the Hall and to determine what the State of the Meal is. He (usually a he, people) decides that 100 guests who arrived early are more advanced in their meal, and are nearing the final Curd Rice course, which he should send in next. The Late Comers are yet to be served the Saambhaar course.
Now, here is the interesting part. If we recognize that the Meal has a sequence of Courses, then the Sequence of Courses and the Sequence of Guests are mutually inverted: the EARLY people are eating the LATER course, and the LATER people are eating the EARLY course!!
So here we complete the metaphor: (whew!):
- The (Meal) Course Sequence is our
Impulse Response - All Guests are the
InputSequence - The State of the Meal is the
Outputof the System, and is theConvolutionof the Course Sequence with the Guest Sequence.
To obtain the proper Output, we need to time-invert the Meal Sequence so that the State of the Meal is a weighted count/sum/integral of the two.
Now we are ready for the Code!!
Convolution in Code
In R, we can use a terrific package called gsignal that allows us to a lot of Signal Processing stuff.
In the following, we will generate a [Butterworth Lowpass filter] that filters out everything that is above 10Hz. We will plot its Impulse Response and then give it an iput of a 2.3Hz sinewave + Noise.
We will then observe the input and the output and compare them.
Show the Code
# library(gsignal)
fs <- 4096 # sampling frequency
bf <- butter(n = 5, w = 10 / (fs / 2), type = "low") # 10 Hz low-pass filter (10/fs
t <- seq(0, 1, len = fs) # 1 second sample
x <- sin(2 * pi * t * 2.3) + 0.25 * rnorm(length(t)) # 2.3 Hz sinusoid+noise
z <- filter(bf, x) # apply filter
# Outputs
btr <- impz(bf, fs = fs)
bfr <- freqz(filt = bf, fs = fs)
## Make Plots
## Frequency Response
plot(bfr$w, 20 * log10(abs(bfr$h)),
type = "l", ylim = c(-10, 0),
xlim = c(0, 50), main = "Frequency Response of 10Hz Lowpass Butterworth Filter", ylab = "Magnitude in dB", xlab = "Frequency"
)
## Impulse Response
plot(btr$x, type = "l", main = "Impulse Response of 10Hz Lowpass Butterworth Filter", ylab = "Amplitude", xlab = "Samples")
## input and Output
plot(t, x, type = "l", main = "Input Signal: 2.3Hz Sine + Noise", ylab = "Amplitude", xlab = "Time (s)")
lines(t, z,
type = "l",
main = "Output Signal: Filtered Output",
ylab = "Amplitude", xlab = "Time (s)", col = "red"
)
legend("topright",
legend = c("Input", "Output"),
col = c("black", "red"), lty = 1
)
- Perceptrons are a standard convolution operation.
- Convolution is an operation that is crucial to the operation of Convolutional Neural Networks. The early (spatial) filter layers in a CNN implement a convolution with impulse responses that learn to look for edges, curves and similar canonical pieces in an input image.
- When we generate guitar-like sounds using the Karplus-Strong Guitar Algorithm, we are using a set of filters (with low-pass/band-pass impulse responses) in the feedback loop of a delay-line primed with random noise.
- Convolution can be seen as a series of Vector Dot Products between two vectors sliding past each other.
To be Written Up.