L-Systems

Iterated Functions

Fractals

L-Systems

Algorithmic Patterns

Symmetry

Published

May 2, 2024

Modified

July 19, 2025

Trees

“I think that I shall never see
A poem lovely as a tree.
A tree whose hungry mouth is prest
Against the earth’s sweet flowing breast;
A tree that looks at God all day,
And lifts her leafy arms to pray;
A tree that may in Summer wear
A nest of robins in her hair;
Upon whose bosom snow has lain;
Who intimately lives with rain.
Poems are made by fools like me,
But only God can make a tree.”

— Joyce Kilmer, 1915

Inspiration

Introduction

Trees are fractal in nature, meaning that patterns created by the large structures, such as the main branches, repeat themselves in smaller structures, such as smaller branches…. a universal growth pattern first observed by Leonardo da Vinci 500 years ago: a simple yet startling relationship that always holds between the size of a tree’s trunk and sizes of its branches.

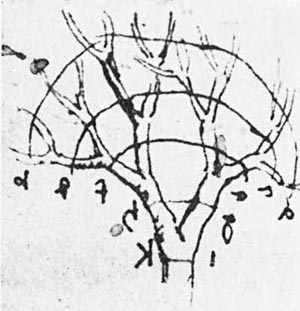
An Introduction to L-Systems

From Job Talle’s Website:

Lindenmayer systems were originally conceived by Hungarian biologist Aristid Lindenmayer while studying algae growth. He developed L-systems as a way to describe the growth process of algae and simple plants. The result was a type of language in which the recursive and self similar properties of organism growth can be expressed. Indeed, L-systems can be used to generate natural patterns, but well known mathematical patterns can also be written as an L-system. In this article, I will explain different flavors of L-systems, and I will demonstrate them by rendering 2D Lindenmayer systems and 3D Lindenmayer systems using turtle graphics.

The language is very simple. It consists of symbols (the alphabet) and production rules. The first state of the sentence is called the axiom. The production rules can be applied repeatedly on this axiom to evolve or grow the system. A simple example would be a system with the axiom \(AA\), and the rule \(A→ABA\).

You can see how a self expanding sentence can be analogous to cell division in plants and other biological processes.

\[ axiom: AA \] \[ Production ~ Rule: A --> ABA \]

\[ Iterations:\\\ 1. A\\\ \]

\[ 2. ~\color{magenta}{A}~\color{Black}B~\color{magenta}{A}\\\ \] \[ 3.~\color{magenta}{ABA}~\color{Black}B~\color{magenta}{ABA}\\\ \] \[ 4.~\color{magenta}{ABA}~\color{Black}B~\color{magenta}{ABA}~~\color{Black}B~~\color{magenta}{ABA}~\color{Black}B~\color{magenta}{ABA} \]

L-system Structures thus develop through a process of string rewriting. A string of letters is transformed into a new string of letters using simple rules called productions. The process is repeated indefinitely, each time using the string that was just produced as the source for the next string. Because the strings tend to grow with each rewrite, an L-system can become arbitrarily complex, but always guided by a simple process dictated by a fixed set of simple rules. In this respect, L-systems are a manifestation of Complexity Phenomena.

All right, but how does this become a tree??

Two things need to be done:

Each symbol in the language needs to be mapped to a left branch or a right branch. (with turn angle)
At each application of the production rules, branch size is scaled down by a number.

Image Courtesy Christophe Eloy | University of Provence.

In the Figure 1, the RHS shows a typical figure generated by the L-system language. This figure shows both the LHS and RHS turns, and the fairly rapid reduction in the size of the branches.

Let us see how we can create “Algorithmic Trees”.

Creating Trees using L-systems

We will use the package LindenmayerR to create our tree.

Show the Code

library(tidyverse)
###
library(LindenmayeR)
library(LearnGeom)
library(TurtleGraphics)
options(max.print = 20)

# Lindemayer tree

## Dictionary of Symbols
dictionary <- data.frame(
  symbol = c("F", "f", "+", "-", "[", "]"), # symbol column
  action = c("F", "f", "+", "-", "[", "]"), # action column
  stringsAsFactors = FALSE
)

## Axioms to start and morph
tree_morph_rules <- data.frame(
  inp = c("F"), # starting axiom
  out = c("F[+F][-F]"), # Morphing Rule
  stringsAsFactors = FALSE
)

## Build the Tree with commands
Ltree <- Lsys(
  init = "F",
  rules = tree_morph_rules,
  n = 2,
  verbose = 0, # No progress messages please...
  retAll = FALSE # One Vector output at the end only
)

[[1]]
     start end
[1,]     1   1

[[1]]
  start end    insert
1     1   1 F[+F][-F]

[[1]]
     start end
[1,]     1   1
[2,]     4   4
[3,]     8   8

[[1]]
  start end    insert
1     1   1 F[+F][-F]
2     4   4 F[+F][-F]
3     8   8 F[+F][-F]

## Now draw the tree
drawLsys(
  string = Ltree,
  drules = dictionary,
  stepSize = 10, shrinkFactor = 1.2, # integers shrink!
  ang = 12,
  st = c(50, 10, 90) # Root Position x, y, angle from bottom-left
)

A more complex, and more botanical-looking, tree or seaweed:

## Define Axiom and Mutation Rules
fractal_tree_rules <- data.frame(
  inp = c("X", "F"),
  out = c("F-[[X]+X]+F[+FX]-X", "FF"),
  stringsAsFactors = FALSE
)

## Create the Algorithmic Tree
fractal_tree <- Lsys(
  init = "X", # Axiom
  rules = fractal_tree_rules,
  n = 4,
  verbose = 0,
  retAll = FALSE
)

## Now draw the tree
drawLsys(
  string = fractal_tree,
  drules = dictionary,
  stepSize = 2, # Shrink by half each time
  ang = runif(n = 1, min = 3, max = 30),
  st = c(50, 5, 90), # Origin of tree
  gp = gpar(col = "chocolate4", fill = "honeydew")
)

grid.text("Fractal Seaweed (n = 4)", 0.25, 0.25)

[[1]]
     start end
[1,]     1   1

[[1]]
  start end             insert
1     1   1 F-[[X]+X]+F[+FX]-X

[[1]]
     start end
[1,]     5   5
[2,]     8   8
[3,]    15  15
[4,]    18  18

[[2]]
     start end
[1,]     1   1
[2,]    11  11
[3,]    14  14

[[1]]
  start end             insert
1     5   5 F-[[X]+X]+F[+FX]-X
2     8   8 F-[[X]+X]+F[+FX]-X
3    15  15 F-[[X]+X]+F[+FX]-X
4    18  18 F-[[X]+X]+F[+FX]-X

[[2]]
  start end insert
1     1   1     FF
2    11  11     FF
3    14  14     FF

[[1]]
      start end
 [1,]    10  10
 [2,]    13  13
 [3,]    20  20
 [4,]    23  23
 [5,]    30  30
 [6,]    33  33
 [7,]    40  40
 [8,]    43  43
 [9,]    56  56
[10,]    59  59
 [ reached 'max' / getOption("max.print") -- omitted 6 rows ]

[[2]]
      start end
 [1,]     1   1
 [2,]     2   2
 [3,]     6   6
 [4,]    16  16
 [5,]    19  19
 [6,]    26  26
 [7,]    36  36
 [8,]    39  39
 [9,]    46  46
[10,]    47  47
 [ reached 'max' / getOption("max.print") -- omitted 8 rows ]

[[1]]
  start end             insert
1    10  10 F-[[X]+X]+F[+FX]-X
2    13  13 F-[[X]+X]+F[+FX]-X
3    20  20 F-[[X]+X]+F[+FX]-X
4    23  23 F-[[X]+X]+F[+FX]-X
5    30  30 F-[[X]+X]+F[+FX]-X
6    33  33 F-[[X]+X]+F[+FX]-X
 [ reached 'max' / getOption("max.print") -- omitted 10 rows ]

[[2]]
  start end insert
1     1   1     FF
2     2   2     FF
3     6   6     FF
4    16  16     FF
5    19  19     FF
6    26  26     FF
 [ reached 'max' / getOption("max.print") -- omitted 12 rows ]

[[1]]
      start end
 [1,]    17  17
 [2,]    20  20
 [3,]    27  27
 [4,]    30  30
 [5,]    37  37
 [6,]    40  40
 [7,]    47  47
 [8,]    50  50
 [9,]    63  63
[10,]    66  66
 [ reached 'max' / getOption("max.print") -- omitted 54 rows ]

[[2]]
      start end
 [1,]     1   1
 [2,]     2   2
 [3,]     3   3
 [4,]     4   4
 [5,]     8   8
 [6,]     9   9
 [7,]    13  13
 [8,]    23  23
 [9,]    26  26
[10,]    33  33
 [ reached 'max' / getOption("max.print") -- omitted 74 rows ]

[[1]]
  start end             insert
1    17  17 F-[[X]+X]+F[+FX]-X
2    20  20 F-[[X]+X]+F[+FX]-X
3    27  27 F-[[X]+X]+F[+FX]-X
4    30  30 F-[[X]+X]+F[+FX]-X
5    37  37 F-[[X]+X]+F[+FX]-X
6    40  40 F-[[X]+X]+F[+FX]-X
 [ reached 'max' / getOption("max.print") -- omitted 58 rows ]

[[2]]
  start end insert
1     1   1     FF
2     2   2     FF
3     3   3     FF
4     4   4     FF
5     8   8     FF
6     9   9     FF
 [ reached 'max' / getOption("max.print") -- omitted 78 rows ]

Head off to https://www.cs.unm.edu/~joel/PaperFoldingFractal/paper.html. Download the .jar file and save it say in your Documents folder. Open and play. Instructions are on the website. Make note of how the scaling factor works here.

Some suggestions!! Note the alphabet!!!

Col1 Col2

Col1	Col2
Pythagorean Tree: Axiom: [++!++!++!]xy Production Rules: x = [-[!++!++!++!]!xy y = [+![!++!++!++!]!xy `- startAngle: 0 - turnAngle: 45.0 - growth : 1.408`	\|
B. Krishna’s Anklets: Axiom: ++af-h-f+h `- f` ## h f++h++f-h-f++h++f-h-f++h Production Rules: f = f - h - f ++ h ++ f - h - f startAngle: 0 turnAngle: 45.0 growth:1.0

Pythagorean Tree:

Axiom: [++!++!++!]xy
Production Rules:
- x =
[-[!++!++!++!]!xy
- y =

[+![!++!++!++!]!xy

-   startAngle: 0
-   turnAngle: 45.0
-   growth : 1.408

B. Krishna’s Anklets:

Axiom: ++af-h-f+h
```
-   f
```
- ## h
  
  f++h++f-h-f++h++f-h-f++h
Production Rules:
- f = f - h - f ++ h ++ f - h - f
- startAngle: 0
- turnAngle: 45.0
- growth:1.0

Design Principles for L-Systems

Pick a set of symbols. i.e. our alphabet (say two or three letters of the alphabet)
Map these to specific movements in the growth of the tree
Decide on an axiom. It can include one or more of the symbols.
Decide on a (set of) production rules. These should generate all the symbols in our alphabet. (Why?)
Decide on a scaling factor
Apply the production rules multiple times starting with the axiom, develop an extensive string using this recursion
Plot the resulting string, scaling the individual recursions by the scaling factor.

Wait, But Why?

By making use of “just sufficient randomness” in a few parameters, it is possible to generate very organic-looking trees
These tree-like layouts can show up in a surprising number of places, such as transport networks, residential layouts.
The multiple iterations generated from a few simple rules embody all the complexity of a language.
Trees become a great metaphor for a diverse set of things and ideas.

References

Job Talle. Lindenmayer Systems https://jobtalle.com/lindenmayer_systems.html
C. J Jennings. L-systems. https://cgjennings.ca/articles/l-systems/
Joel Castellanos. Fractal Grower: Java Software for Growing Lindenmayer Substitution Fractals (L-systems). https://www.cs.unm.edu/~joel/PaperFoldingFractal/paper.html
Paul Bourke. L systems User Notes. https://paulbourke.net/fractals/lsys/
Przemysław Prusinkiewicz and Aristid Lindenmayer. The Algorithmic Beauty of Plants. Springer-Verlag, 1990.